- Author Matthew Elmers [email protected].
- Public 2023-12-16 21:49.
- Last modified 2025-01-24 09:17.

What determines accuracy - one of the main characteristics of a weapon? Obviously, from the quality of the barrel and cartridge. Let's postpone the cartridge for now, but consider the physics of the process.
Take a metal rod or tube made of elastic metal and rigidly fix it in a massive base. So we get a model of the device under study. Now, if we hit the rod, it does not matter in what place and in what direction, either pull it back, or squeeze it, or, finally, inserting a cartridge into the tube and firing a shot, we will see that the rod (barrel) has come into a damped oscillatory motion. These vibrations are decomposed into the simplest, and each type of such a simple vibration of the barrel will affect the accuracy (accuracy) of shooting in its own way.
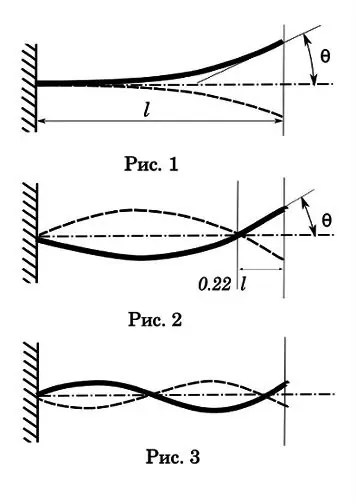
Let's start with the first-order or pitch vibrations. As you can see (Fig. 1), such an oscillation has only one node at the attachment point, the largest amplitude, the longest decay time and the longest oscillation time of one period. This time is 0.017-0.033 sec. The bullet travel time through the bore is 0, 001-0, 002 sec. That is, significantly less than the cycle of one oscillation, which means that this type of oscillation does not have a significant effect on the accuracy of a single shot. But with automatic shooting, an interesting picture can turn out. Let's say the rate of fire is 1200 rds / min, i.e. time of one cycle - 0.05 sec. With a period of oscillations of the first order of 0, 025 sec, we have a multiple ratio of frequencies. And this is an indispensable condition for resonance with all the ensuing consequences - the weapon begins to shake with such force that it can fall apart.
Let's move on to oscillations of the second order (Fig. 2). But I suggest that humanities students first conduct an experiment in order to eliminate the shortcomings of education in the field of physics. You need to take a little boy (you can a girl), put him on a swing and swing. Before you is a pendulum. Stand to the side of the swing and try to hit the boy with the ball. After a series of attempts, you will come to the conclusion that it is best to hit when the target is in the first phase of oscillation - the maximum deviation from the equilibrium point. At this point, the target has zero speed.
Let's look at the second order diagram. The second vibration node is located approximately 0.22 from the end of the barrel. This point is a law of nature, it is impossible to create such vibrations for the cantilever beam so that the second node falls on the free end. It is where it is and does not depend on the length of the barrel.
The amplitude of oscillations in the second-order scheme is lower, but the oscillation time is already comparable to the time of passage of the bullet through the bore - 0, 0025-0, 005 sec. So for single shooting this is already of interest. To make it clear what we are talking about, imagine a barrel 1 meter long. The bullet travels through the entire barrel in 0, 001 seconds. If the oscillation period is 0.004 sec, then by the time the bullet leaves the barrel, the barrel will reach its maximum bend in the first phase. The question for the humanities is - at what point (in what phase) is it best to shoot a bullet out of the barrel to ensure consistency of results? Remember the swing. At the zero point, the vector of the trunk deflection velocity is maximum. It is more difficult for a bullet to hit this point on the cut of the trunk, it also has its own error in speed. That is, the best moment for the bullet to fly out will be when the barrel is at the highest point of the first deflection phase - as in the figure. Then insignificant deviations in bullet velocity will be compensated by a longer time spent by the barrel in its most stable phase.
A graphical representation of this phenomenon can be clearly seen in the diagram (Fig. 4-5). Here - Δt is the time error with which the bullet crosses the muzzle of the barrel. In fig. 4 is ideal when the average bullet take-off time coincides with the zero phase of the barrel oscillation. (Mathematicians! I know that the velocity distribution is non-linear.) The shaded area is the angle of spread of the trajectories.
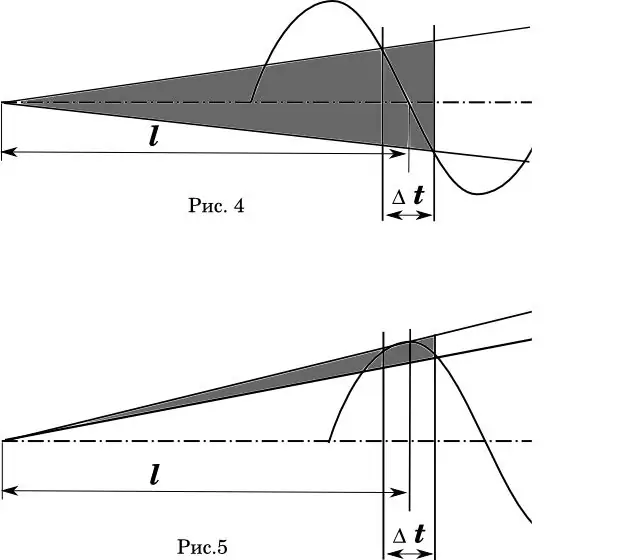
In Fig. 5, the barrel length and velocity error remain the same. But the phase of the barrel bending is shifted so that the average time of departure coincides with the maximum deflection of the barrel. Are comments superfluous?
Well, is it worth the candle? How severe can the deviations caused by second-order oscillations be? Serious and very serious. According to the Soviet professor Dmitry Aleksandrovich Ventzel, in one of the experiments the following results were obtained: the radius of the median deviation increased by 40% with a change in the barrel length by only 100 mm. For comparison, a high-quality barrel treatment can improve accuracy by only 20%!
Now let's take a look at the formula for the vibration frequency:
where:
k - coefficient for second-order oscillations - 4, 7;
L is the barrel length;
E is the modulus of elasticity;
I is the moment of inertia of the section;
m is the mass of the trunk.
… and proceed to the analysis and conclusions.
The obvious conclusion from Figures 4-5 is bullet velocity error. It depends on the quality of the powder and its weight and density in the cartridge. If this error is at least a quarter of the cycle time, then everything else can be given up. Fortunately, science and industry have achieved very great stability in this matter. And for the more sophisticated (in benchrest, for example) there are all the conditions for self-assembly of cartridges in order to fit the bullet's exit phase exactly to the barrel length.
So, we have a cartridge with the lowest possible speed variation. The barrel length was calculated based on its maximum weight. The question of stability arises. We look at the formula. What variables affect the change in the frequency of oscillation? Barrel length, modulus of elasticity and mass. The barrel heats up during firing. Can heat change barrel length so that accuracy is affected. Yes and no. Yes, since this figure lies within hundredths of a percent for a temperature of 200 C. No, since the change in the elastic modulus of steel for the same temperature is about 8-9%, for 600C it is almost twice. That is, many times higher! The barrel becomes softer, the bending phase of the barrel shifts forward by the moment the bullet leaves, the accuracy drops. Well, what does a thoughtful analyst say? He will say that it is impossible to get maximum accuracy on one barrel length in cold and hot mode! The weapon may have a better performance with either a cold or hot barrel. Accordingly, two classes of weapons are obtained. One is for ambush actions, when the target must be hit from the first - "cold" shot, because the accuracy of the second will be worse due to the inevitable heating of the barrel. In such a weapon there is no urgent need for automation. And the second class is automatic rifles, the barrel length of which is tailored to the hot barrel. In this case, a possible miss due to the low accuracy of a cold shot can be compensated for by a quick subsequent hot and more accurate shot.
EF Dragunov knew the physics of this process very well when he was designing his rifle. I suggest that you familiarize yourself with the story of his son Alexei. But first, someone will have to break their brains. As you know, two samples of Konstantinov and Dragunov approached the final of the competition for a sniper rifle. The designers were friends and helped each other in everything. So, Konstantinov's rifle was "tuned" to cold mode, Dragunov's rifle to "hot". Trying to improve the accuracy of the rival's rifle, Dragunov fires his rifle with long pauses.

Let's look at the formula again. As you can see, the frequency also depends on the mass of the barrel. The mass of the trunk is constant. But hard contact with the forend produces an unpredictable positive feedback to the barrel. The system - barrel-forend-arm (support) will have a different moment of inertia (a set of masses relative to the attachment point), which means that this can also cause a phase shift. This is why athletes use soft support. The same feature is associated with the application of the principle of "suspended barrel", when the forend of the weapon does not have a hard contact with the barrel and is rigidly attached to it (the weapon) only in the area of the receiver, and the second end either does not touch the barrel at all or touches through a spring-loaded joint (SVD).
Final thought. The fact that with the same barrel length it is impossible to obtain the same accuracy at different temperatures gives an excellent reason to stretch your brains. It is only necessary to change the length and / or mass of the barrel when the temperature of the barrel changes. Without changing either the length or the weight of the barrel. From the point of view of the humanities, this is a paradox. From the point of view of a techie, an ideal task. The whole life of a designer is connected with the solution of such problems. The Sherlocks are resting.






