- Author Matthew Elmers [email protected].
- Public 2024-01-11 04:35.
- Last modified 2025-01-24 09:17.
In this article we will try to understand the armor penetration of the guns of the Bayern, Rivenge, and Pennsylvania battleships, as well as the comparative quality of German, American and British armor. It is extremely difficult to do this, because the data on the American 356-mm, German 380-mm and British 381-mm cannons are very fragmentary and incomplete, and sometimes contradict each other, but we will try anyway.
What exactly is the problem? Let's see how most fans of naval (and not only) history compare the armor penetration of certain weapons. For example: in one publication devoted, for example, to English dreadnoughts, there is information that a British 381-mm projectile from the First World War pierced 381-mm armor plate at a distance of about 70 cables. In another edition, devoted to the already German "capital" ships - that a similar German 380-mm projectile "mastered" 350 mm armor with only 67, 5 cables. It seems to follow from this that the English cannon is more powerful - this is precisely the conclusion made.
However, in reality, comparing data like this in this way is very easy to get into trouble.
Are the above data obtained as a result of actual shooting, or are they calculated using armor penetration techniques? If these are the results of actual shooting, were the conditions identical for both guns? If the armor penetration was obtained by calculation, then were the same methods used? Are the obtained data the result of the work of specialists from the relevant ministries and departments, or is it the result of calculations by historians who have taken up a calculator? It is clear that in the second case the accuracy will be much lower … You don't have to go far for examples: let's take the famous monograph by S. Vinogradov, "Superdreadnoughts of the Second Reich" Bayern "and" Baden ". In Appendix No. 2, the respected historian, together with V. L. Kofman make a large amount of calculations in order to compare the capabilities of the battleships Rivenge and Bayern. But alas, it is enough to look at the table of parameters for 15-inch guns (p. 124) and we will see that, according to the calculations of respected authors, an English 381-mm gun with an elevation angle of 20, 25 degrees has a range of only 105 cables, that is, about 19, 5 thousand m. While foreign sources for the same initial speed (732 m / s) and a slightly lower elevation angle (20 degrees) give much longer distances - 21, 3-21, 7 thousand m. Of course however, such deviations from real values have the most negative effect on the calculation results.
But even if the sources present the results of calculations of specialists, the accuracy of which there is no doubt, another factor arises that complicates the comparison: the point here is the quality of armor. It is clear that the same British, when calculating armor penetration when designing a particular dreadnought, used the corresponding indicators of British armor, the Germans - respectively, German, etc. And the armor of different countries may differ in durability, but this is still half the trouble: after all, in a single country, the same Krupp armor was constantly being improved. Thus, it turns out that the calculations of artillery systems, made, for example, in England, and seemingly for the same Krupp armor, but made at different times, may turn out to be incomparable. And if we add to this the almost complete absence of serious work on the evolution of the armor case in various countries of the world …
In general, a more or less reliable comparison of armor penetration is not as simple a task as it might seem at first glance. And, in an amicable way, a layman (which, without a doubt, is the author of this article) is better not to take on this matter. But, alas - to our deep regret, the pros are somehow in no hurry to deal with these issues, so … as they say, in the absence of stamped paper, we write in plain text.
Of course, it is no longer possible to carry out full-scale tests of the above-mentioned artillery systems, so our destiny is calculations. And if so, then it is necessary to say at least a couple of words about the armor penetration formulas. If modern calculation methods are published, then only in closed editions, and in popular literature, the Jacob de Marr formula is usually given. It is interesting that Professor of the Naval Academy L. G. Goncharov, in his 1932 artillery textbook, called it the Jacob de Marr formula. This formula, along with many others, was widespread at the beginning of the last century, and, I must say, it is quite accurate - perhaps it is even the most accurate among similar formulas of those years.
Its peculiarity lies in the fact that it is not physical, that is, it is not a mathematical description of physical processes. De Marr's formula is empirical, it reflects the results of experimental shelling of iron and steel-iron armor. Despite this "unscientific nature", de Marr's formula showed a better approximation to the actual results of shooting and on Krupp armor than other common formulas, and therefore we will use it for calculations.
Those interested will find this formula in the appendix to this article, but there is no need to force everyone who reads this material to understand it - this is not necessary to understand the conclusions of the article. We only note that the calculation uses very simple and familiar concepts to all those interested in the history of military fleets. These are the mass and caliber of the projectile, the thickness of the armor, the angle at which the projectile hits the armor, and the velocity of the projectile at the moment it hits the armor plate. However, de Marr, of course, could not limit himself to the above parameters. After all, the penetration of a projectile depends not only on its caliber and mass, but also, to a certain extent, on its shape and the quality of the steel from which it is made. And the thickness of the armor plate, which the projectile is able to overcome, depends, of course, not only on the performance of the projectile, but also on the quality of the armor. Therefore, de Marr introduced a special coefficient into the formula, which, in fact, is designed to take into account the indicated qualities of armor and a projectile. This coefficient rises with an increase in the quality of armor and decreases with a deterioration in the shape and quality of the projectile.
As a matter of fact, the main difficulty in comparing the artillery systems of different countries just "rests" on this very coefficient, which we, in the future, will simply call (K). We will need to find it for each of the above tools - if, of course, we want to get a somewhat correct result.
So, let us first take fairly widespread data on the armor penetration of the German 380-mm / 45 gun "Bayern", according to which the gun at a distance of 12,500 m (those same 67, 5 cables) could penetrate 350 mm of armor. We use a ballistic calculator to find the parameters of a 750-kg projectile, with an initial speed of 800 m / s at the moment of impact on the armor: it turns out that such a projectile will hit a strictly vertically positioned armor plate at an angle of 10, 39 degrees, with a speed of 505, 8 m / sec. A small disclaimer - hereinafter, when we talk about the angle of impact of the projectile, we mean the so-called "angle from the normal". "Normal" is when the projectile hits the bonneplite strictly perpendicular to its surface, that is, at an angle of 90 degrees. Accordingly, the projectile hit at an angle of 10 degrees.from the normal means that it hit the slab at an angle of 80 degrees. to its surface, deviating from the "reference" 90 degrees. by 10 degrees.
But back to the armor penetration of the German gun. The coefficient (K) in this case will be approximately (rounded to the nearest integer) equal to 2,083 - this value should be considered quite normal for armor of the First World War era. But here one problem arises: the fact is that the source of data on armor penetration is the book "German Capital Ships of World War Two", where the 380-mm / 45 gun of the Bayern was compared with the main caliber of the battleship "Bismarck". And could it not be that the calculation took into account the indicators of the Krupp armor, created in the interval between the two world wars, which was much stronger than the one that was installed on the Bayenne, Rivenge and Pennsylvania? Moreover, the electronic encyclopedia navweaps reports that there is evidence that at a distance of 20,000 m German 380-mm shells were able to penetrate 336 mm armor plate, and we are talking about armor of the First World War era.
Well, we think: at 20 km, the angle of incidence will be 23.9 degrees, the speed of the projectile on the armor is 410.9 m / s, and the coefficient (K) - some unfortunate 1618, which does not at all fit into the armor resistance values era of WWI. A similar result generally brings German-made Krupp armor closer to homogeneous armor resistance … Obviously, the navweaps data contain some kind of error.
Let's try then to use another source of information. Until now, we have used the calculated data, and now we will try to compare them with the results of actual tests of the German 380-mm / 45 cannon: those are given by S. Vinogradov in the above-mentioned monograph devoted to German battleships.
It describes the consequences of 3 shots with armor-piercing projectiles, against armor plates with a thickness of 200, 290 and 450 mm, the latter being the most interesting for us: a projectile weighing 734 kg hit the armor plate at an angle of 0 (that is, at 90 degrees to the surface) and at a speed of 551 m / s punched 450 mm through the slab. A similar result corresponds to the coefficient (K) 1 913, but, in fact, it will be slightly lower, because the Germans found their projectile as much as 2 530 m behind the obstacle it pierced, and - in general. Alas, not having any data on how much of this distance the projectile flew through the air, how much - "rode" on the ground, it is absolutely impossible to determine the energy stored by it after armor penetration.
Let's now take the British 381 mm / 42 artillery system. Alas, the data on its armor penetration is rather vague: for example, V. L. Kofman, there is a mention of the fact that these British guns pierced armor, thickness of their own caliber at a distance of about 70 cables. But with what projectile and with what initial velocity? Taking into account that the reference is contained in the monograph dedicated to the battle cruiser "Hood", and refers to the period of creation of this ship, it can be assumed that we are talking about an 871 kg shell. However, another question arises here: the official initial speed of such a projectile was 752 m / s, but some calculations by the British were carried out at a lower speed of 732 m / s, so what value should we take? However, whichever of the indicated speeds we take, the coefficient (K) will fluctuate within 1 983 - 2 048, and this is higher than we calculated for the value (K) for the German gun. It can be assumed that this speaks of the superiority of the quality of the British armor in comparison with the German one … or is it that the geometric shape of the German projectile was better suited for penetrating armor? Or maybe the whole point is that the data of V. L. Kofman are calculated values, but in practice, would British shells achieve a better result?
Well, we have at our disposal data on the results of the shelling of the battleship "Baden"

So, one of the British shells, hitting at an angle of 18 degrees. at a speed of 472 m / sec., "overpowered" 350 mm frontal armor of the German main-caliber turret. These data are all the more valuable because in this case, not British, but German armor was subjected to shelling, that is, the tests of 381-mm / 42 and 380-mm / 45 guns are, thus, in a single coordinate system.
Alas, they do not help us too much. If we assume that the English shell pierced the German tower, as they say, “with the last bit of strength,” and if there were 351 mm armor, it would have failed, then his (K) would be equal to 2,021. It is interesting, by the way, that S. Vinogradov states that the British projectile, which penetrated the 350 mm frontal armor of the German tower, was not subsequently found, but in fact the report states something else - it exploded, and there is a description of where the fragments flew in the tower.
Of course, we have no absolute grounds for assuming that this penetration was the limit for a 381-mm projectile, or even close to that. But nevertheless, according to some indirect signs, it can be assumed that this was exactly the case. Another hit “hints” at this: a British 871 kg projectile hitting a 350 mm barbet at an angle of 11 degrees, although it was able to make a hole in the armor with a diameter of 40 cm, it did not get inside the barbet itself, bursting in the process of overcoming the armor. In this case, the hit occurred almost in the very center of the barbet, that is, the curvature of the armor plate, if it had any influence, it was the very minimum.
From all of the above, one can try to draw some conclusions, but, due to the fragility of the evidence base, they, of course, will be highly speculative.
Conclusion 1: German armor during the First World War roughly matched the British in terms of durability. This conclusion is valid if the statement of V. L. Kofman that the English 381 mm / 42 gun was capable of penetrating armor equal to its caliber by 70 kbt, and if we were not mistaken in the assumption that the penetration of 350 mm of the frontal plate of the German turret at an angle of 18 degrees and a speed of 472 m / s … is the limit or very close to the penetration limit of the British 381 mm projectile.
Conclusion 2nd. Apparently, the shape and quality of the German 380-mm projectile provided it with better armor penetration than the English one. Based on the above data, we can assume that the coefficient (K) of the British 381 mm projectile when firing at German armor was about 2,000, while the German 380 mm projectile was about 1,900. If our first one is correct the conclusion that the armor resistance of British and German armor is approximately equivalent, it is obvious that the only reason for the lower coefficient (K) can only be the projectile itself.
Why could a German shell be better? Its caliber is slightly smaller, by one millimeter, but, of course, this could hardly have any significant effect. The calculation shows that with the same mass (750 kg), a change in caliber by 1 millimeter will lead to an increase in armor penetration by 1.03 millimeters. The German projectile is also shorter - its length was 3.5 caliber, while the length of the British "Greenboy" is 4 caliber. There may have been other differences as well. Of course, the quality of the steel from which the projectile is made plays a significant role here.
Let us now calculate the armor penetration of the German and British guns for a distance of 75 cables - the generally accepted distance for a decisive battle, where one could expect a sufficient number of hits to destroy an enemy ship of the line.
At the indicated distance, 871 kg of a British 381-mm / 42 cannon shell, fired at an initial speed of 752 m / s, hit the vertically positioned armor plate at an angle of 13.05 degrees, and its speed "on the plate" was 479.6 m / s … With (K) equal to 2,000, according to the formula of Jacob de Marr, the armor penetration of the British projectile was 376, 2 mm.
As for the German shell, everything is a little more complicated. If our conclusion that it surpassed English in terms of armor penetration is correct, then the capabilities of the German 380-mm / 45 gun on 75 cables were very close to the English fifteen-inch gun. At this distance, the German 750 kg projectile hit the target at an angle of 12.42 degrees at a speed of 482.2 m / s, and at (K) equal to 1,900, the armor penetration was 368.9 mm. But if the author of this article is still mistaken, and for the German gun it is worth using the same coefficient as for the English gun, then the capabilities of the 380-mm projectile fall to 342.9 mm.
Nevertheless, according to the author, the armor penetration of the German projectile is closest to 368, 9 mm (after all, practical firing yielded a coefficient of 1 913, despite the fact that the projectile flew then 2.5 km), but the armor penetration of the English projectile may be slightly lower calculated. In general, it can be considered that at a distance of 75 cables, the British and German artillery systems are quite comparable in terms of armor penetration.
But with the American 356 mm / 45 gun, everything turned out much more interesting. The previously cited data for shells weighing 680 kg should be considered canonical in the Russian-language literature.
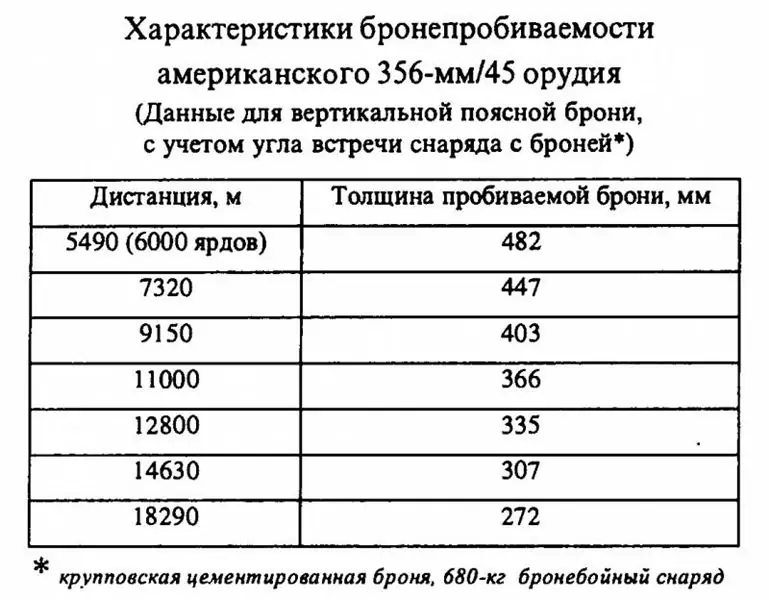
As a matter of fact, the values indicated in it seem to lead to completely obvious conclusions: if even the 680-kg shells that appeared in the United States after 1923 are inferior in armor penetration to their 380-381-mm European "colleagues", then what really talk about the earlier 635 kg shells, which were equipped with 356-mm artillery of American dreadnoughts! They are lighter, which means they lose speed faster in flight, while their initial speed did not exceed heavier shells, and in terms of shape and quality, the 1923 ammunition should have an advantage. It is as clear as day that the American "Pennsylvania" at the time of entry into service were inferior in terms of armor penetration to the British and German dreadnoughts. Well, it's obvious, isn't it?
This is exactly the conclusion the author made, considering the capabilities of American fourteen-inch guns in the article "Standard" battleships of the USA, Germany and England. American "Pennsylvania" ". And then he picked up a calculator …
The fact is that the calculation according to the de Marra formula showed that the American 356-mm / 45 guns had the armor penetration indicated in the table with a coefficient (K) equal to 2,317! In other words, the American 680 kg shells shown in the table showed the results when exposed to armor that was not created in the era of the First World War, but much later and stronger samples.
It is difficult to say how much the strength of armor protection has increased in the interval between the first and second world wars. In Russian-language sources on this occasion there are only brief and often contradictory references, on the basis of which it can be assumed that the strength of Krupp's armor has increased by about 20-25%. Thus, for large-caliber shells of the era of the First World, the growth of the coefficient (K) will be from 1,900 - 2,000 to 2,280 - 2,500, but here it must be remembered that with an increase in the quality of armor protection, of course, the quality of shells also increased, and therefore for heavy Ammunition of the Second World War (K) may be less. Therefore, (K) in the amount of 2,317 for post-war shells, naturally improved taking into account the experience gained earlier, looks quite organic, but for the armor of the era of the Second World War, not the first.
But by setting the coefficient (K) for the American 680-kg shells at the level of 2,000, that is, by bringing the quality of armor protection to the era of the First World War, for a distance of 75 cables we will get armor penetration at the level of 393.5 mm, that is, higher than that of the British and German fifteen-inch guns!

Conversion to 635 kg projectile gives a very insignificant correction - the ballistic calculator showed that at a distance of 75 cables, having an angle of incidence of 10, 82 degrees. and the speed "on the armor" 533, 2 m at (K) equal to 2,000, the American projectile penetrates the armor of the era of the First World War, 380 mm thick, that is, significantly more than its own caliber!
On the other hand, it is quite possible that such a calculation is still not entirely correct. The fact is that, according to some reports, the coefficient (K) for the same armor decreases with an increase in the caliber of the projectile. So, for example, in our calculations, the maximum value (K) for the German 380-mm / 45 artillery system, obtained by calculation and published in sources, is 2,083. At the same time, the calculations for the German 305-mm / 50 guns, which were installed on Kaiserlichmarine ships starting with the Heligolands, the data from sources on armor penetration give (K) at the level of 2,145. Accordingly, it is possible that the 356-mm / 45 guns (K) = 2,000 we took for calculating the armor penetration of American guns is still too small.
In addition, unfortunately, the author does not have any "clues" to compare the armor resistance of the American Krupp armor with its European counterparts. There is nothing left but to consider it equivalent to German and English armor protection, although this, of course, may not be the case.
Let's summarize all these rather chaotic data. Taking into account the errors of the "methods" used in the calculations, it can be assumed with a high degree of probability that The armor penetration of the vertical armor protection of the main caliber guns of the battleships Rivenge, Bayern and Pennsylvania at a distance of 75 cables was approximately the same, and was approximately 365-380 mm.
Despite a bunch of assumptions, the data at our disposal still allow us to draw some conclusions regarding vertical armor protection. But with breaking through horizontal barriers, which are armored decks, everything is much more complicated. The fact is that Jacob de Marr, unfortunately, did not bother at all to create a formula for determining the strength of the horizontal defense. Its basic formula, adapted to modern types of armor, is only suitable for calculating cemented armor with a thickness of over 75 mm. This formula is given in Appendix No. 1 to this article, and all the previous calculations in the article were made using it.
But the decks of ships of those years were protected not by cemented (heterogeneous) but by homogeneous armor, which lacked a surface hardened layer. For such armor (but - installed vertically!) A different formula is used, intended for evaluating non-cemented armor plates with a thickness of less than 75 mm, it is given in Appendix No. 2.
I would like to note that both of these formulas are taken from a more than serious source: “The course of naval tactics. Artillery and Armor 1932, author - Professor of the RKKA Naval Academy L. G. Goncharov, one of the leading experts in the pre-war USSR in the field of naval artillery.
And alas, none of them are suitable for assessing the durability of horizontal protection. If we use the formula for cemented armor, then at a distance of 75 cables we get scanty armor penetration: 46.6 mm for 381 mm / 42 British, 39.5 mm for 380 mm / 45 German, and 33.8 mm for 356 mm / 45 American guns. If we use the second formula for non-cemented armor, then we get that when hit at an angle typical for a distance of 75 cables, all three artillery systems easily penetrate 74 mm armor plate, after which retaining a huge supply of kinetic energy - for example, the English 381- mm, a projectile to penetrate armor of this thickness at a distance of 75 cables will have a speed of 264.5 m / s, while its speed will be 482.2 m / s. If we ignore the limitation on the thickness of the armor plate, it turns out that the British 381-mm projectile, according to the above formula, is capable of penetrating deck armor with a thickness of over 180 mm! Which, of course, is completely impossible.
If we try to refer to the test results of the Bayern-class battleship, we will see that the armor-piercing 871 kg British shells twice hit the horizontal armor of the towers, which had a thickness of 100 mm at an angle of 11 degrees, which corresponds to a distance of 67.5 cables for a projectile with an initial speed of 752 m / s and 65 cables - for a projectile with an initial speed of 732 m / s. Both times the armor was not pierced. But in one case, the projectile, having ricocheted, made a notch in the armor with a depth of 70 cm, that is, the plate was very strongly bent. And in the second, although the shell, again, ricocheted, the armor was not only concave by 10 cm, but also torn.

The similar nature of the damage suggests that, although the German 100 mm armor provided protection at the indicated distances, it was, if not at the limit of the possible, then very close to that. But the calculation according to the formula for cemented armor gives armor penetration of only 46.6 mm at a greater distance, where the angle of incidence will be higher, and, accordingly, it would be easier for the projectile to penetrate the deck armor. That is, according to the formula, it turns out that the 100 mm deck should have jokingly and with a large margin of safety reflect English shells - however, practice does not confirm this. At the same time, according to calculations using the formula for non-cemented armor, it turns out that the roofs of the Baden's main caliber should have been easily pierced, and - with a large supply of projectile energy - which, again, is not at all confirmed by practice.
I must say that such inaccuracies in the calculations have a completely logical explanation. As we said earlier, de Marr's formulas are not a mathematical description of physical processes, but are just a fixation of the patterns obtained when testing armor. But vertical armor protection, not horizontal, was tested, and it is not at all surprising that the patterns in this case simply stop working: for horizontally located armor, into which shells hit at a very small angle to their surface, these patterns, of course, are completely different.
The author of this article came across opinions "on the Internet" that de Marr's formulas work effectively at angles of deviation from the normal no more than 60 degrees, that is, from 30 degrees to the surface of the slab and more. It can be assumed that this assessment is very close to the truth.
Thus, we have to state with regret that the mathematical apparatus available to the author does not allow performing any reliable calculations of the horizontal protection resistance of the battleships Rivenge, Bayern and Pennsylvania. In view of the above, it will be difficult to use the data on the armor penetration of horizontal armor given in various sources - as a rule, they are all based on the same calculations according to de Marr's formulas and are incorrect.






